2718: T3 围圈传球
内存限制:128 MB
时间限制:1.200 S
评测方式:文本比较
命题人:
提交:15
解决:3
题目描述
小$W$ 决定和他的朋友们一起玩个游戏。$n$ 个人围成一圈。
$n$ 个人按照顺时针的方向从 $1$ 编号到 $n$。
一开始,球在第 $x$ 个人手中,然后不断地进行顺时针或者逆时针传递。
每次传递规定顺时针或者逆时针,和传递的距离。
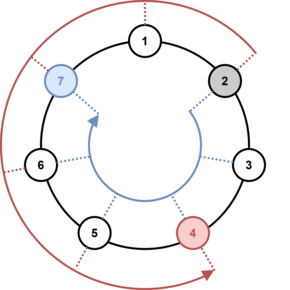
例如:如果有 $7$ 个小朋友玩这个游戏,现在球到第 $2$ 个小朋友手中,选择顺时针传递 $5$ 的距离,那么球就到编号为 $7$ 的小朋友手中;选择逆时针传递 $5$ 的距离,那么球就到编号为 $4$ 的小朋友手中。
游戏将进行 $m$ 轮(进行 $m$ 次传递),但是 小$W$ 只记得传递的距离和 **一些** 传递的方向。
请问进行了 $m$ 轮传递之后,球到了谁的手中,需要输出所有的可能性。
$n$ 个人按照顺时针的方向从 $1$ 编号到 $n$。
一开始,球在第 $x$ 个人手中,然后不断地进行顺时针或者逆时针传递。
每次传递规定顺时针或者逆时针,和传递的距离。
例如:如果有 $7$ 个小朋友玩这个游戏,现在球到第 $2$ 个小朋友手中,选择顺时针传递 $5$ 的距离,那么球就到编号为 $7$ 的小朋友手中;选择逆时针传递 $5$ 的距离,那么球就到编号为 $4$ 的小朋友手中。

游戏将进行 $m$ 轮(进行 $m$ 次传递),但是 小$W$ 只记得传递的距离和 **一些** 传递的方向。
请问进行了 $m$ 轮传递之后,球到了谁的手中,需要输出所有的可能性。
输入
第一行包含三个正整数 $n,m,x\ (1\le x \le n)$,分别表示小朋友的数量、传递的次数、球一开始在谁手中。
接下来 $m$ 行包含每次传递的信息,每行包括一个整数 $r_i\ (1\le r_i\le n-1)$,表示第 $i$ 次传递的距离;以及一个符号 $c_i$ ,可以是 "$0$"、"$1$"、"$?$":
- 如果 $c_i =$ '$0$',则第 $i$ 次是顺时针传递的
- 如果 $c_i =$ '$1$',则第 $i$ 次是逆时针传递的
- 如果 $c_i =$ '$?$',则第 $i$ 次是忘记了传递方向的,可以是顺时针或逆时针
接下来 $m$ 行包含每次传递的信息,每行包括一个整数 $r_i\ (1\le r_i\le n-1)$,表示第 $i$ 次传递的距离;以及一个符号 $c_i$ ,可以是 "$0$"、"$1$"、"$?$":
- 如果 $c_i =$ '$0$',则第 $i$ 次是顺时针传递的
- 如果 $c_i =$ '$1$',则第 $i$ 次是逆时针传递的
- 如果 $c_i =$ '$?$',则第 $i$ 次是忘记了传递方向的,可以是顺时针或逆时针
输出
在第 $1$ 行输出游戏结束之后,球可能在哪些小朋友手中的数量 $k$
在下一行中,输出 $k$ 个数字,可能在哪些小朋友手中的具体小朋友编号。(升序输出)
在下一行中,输出 $k$ 个数字,可能在哪些小朋友手中的具体小朋友编号。(升序输出)
样例输入 复制
6 3 2
2 ?
2 ?
2 ?样例输出 复制
3
2 4 6提示
```input2
5 3 1
4 0
4 1
1 0
```
```output2
1
2
```
```input3
10 7 4
2 ?
9 1
4 ?
7 0
2 0
8 1
5 ?
```
```output3
4
3 5 7 9
```
## 样例提示
样例 $1$: 三次都是顺时针,最终球到编号 $2$;顺时针、逆时针、顺时针,最终球到编号 $4$;顺时针、逆时针、逆时针,最终球到编号 $6$。能求得,最终球只能在这几个编号的小朋友手中。
样例 $2$:按照每一轮进行模拟即可,最终球只能在编号为 $2$ 的小朋友手中。
## 数据范围
对于全部数据 $1\le n,m\le10^4$,$1\le r_i\le n-1$,$1\le x\le n$。
| 测试点 | $n,m \leq$ | 特殊性质 |
| :---------: | :---------: | :----------------------------------: |
| $1\sim 4$ | $100$ | $c_i$ 不为 '$?$',即每轮传递方向确定 |
| $5\sim 10$ | $500$ | $c_i$ 为 '$?$' 的个数不大于$20$ |
| $11\sim 15$ | $2*10^3$ | 无 |
| $16\sim 20$ | $10^4$ | 无 |
5 3 1
4 0
4 1
1 0
```
```output2
1
2
```
```input3
10 7 4
2 ?
9 1
4 ?
7 0
2 0
8 1
5 ?
```
```output3
4
3 5 7 9
```
## 样例提示
样例 $1$: 三次都是顺时针,最终球到编号 $2$;顺时针、逆时针、顺时针,最终球到编号 $4$;顺时针、逆时针、逆时针,最终球到编号 $6$。能求得,最终球只能在这几个编号的小朋友手中。
样例 $2$:按照每一轮进行模拟即可,最终球只能在编号为 $2$ 的小朋友手中。
## 数据范围
对于全部数据 $1\le n,m\le10^4$,$1\le r_i\le n-1$,$1\le x\le n$。
| 测试点 | $n,m \leq$ | 特殊性质 |
| :---------: | :---------: | :----------------------------------: |
| $1\sim 4$ | $100$ | $c_i$ 不为 '$?$',即每轮传递方向确定 |
| $5\sim 10$ | $500$ | $c_i$ 为 '$?$' 的个数不大于$20$ |
| $11\sim 15$ | $2*10^3$ | 无 |
| $16\sim 20$ | $10^4$ | 无 |