2834: T6-抖音小游戏
内存限制:128 MB
时间限制:1.000 S
评测方式:文本比较
命题人:
提交:10
解决:4
题目描述
有一天,YZT 在刷抖音时看到了一段游戏视频。
这个游戏的名字叫涂色游戏,视频中的游戏界面是一个 $n$ 行 $m$ 列的网格,初始时每一个格子都是白色(用数字 $0$ 表示)。其中每一行的左侧、每一列的上方都有一把带颜色的刷子。玩家点击某个刷子后,这个刷子会将其右侧(或下方)的一整行(或一整列)涂上同一种颜色,**该行(或该列)格子原有的颜色都会被覆盖成新涂上的颜色。**
下图展示的情况可以通过先将第一列涂成红色,然后将第一行涂成蓝色得到,若此时选择将第三列涂成绿色,则图中绿色方框中的格子都会变成绿色。
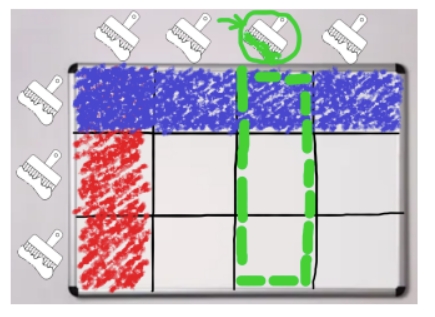
YZT 想用他自己编写的程序来进行视频中的游戏。在编程的过程中,YZT 在涂色逻辑的实现上却遇到了一些困难,于是他向你求助,希望你能帮他完成实现涂色逻辑部分的代码。
首先,YZT 会给你网格的行数和列数 $n, m$,然后给出 $q$ 次操作,每次操作用三个整数 $opt_i, x_i, c_i$ 表示:
- 如果 $opt_i=0$,那么这次操作会将第 $x_i$ **行**涂成颜色 $c_i$。
- 如果 $opt_i=1$,那么这次操作会将第 $x_i$ **列**涂成颜色 $c_i$。
在所有涂色操作结束以后,你需要输出网格中每个位置的颜色是什么。
这个游戏的名字叫涂色游戏,视频中的游戏界面是一个 $n$ 行 $m$ 列的网格,初始时每一个格子都是白色(用数字 $0$ 表示)。其中每一行的左侧、每一列的上方都有一把带颜色的刷子。玩家点击某个刷子后,这个刷子会将其右侧(或下方)的一整行(或一整列)涂上同一种颜色,**该行(或该列)格子原有的颜色都会被覆盖成新涂上的颜色。**
下图展示的情况可以通过先将第一列涂成红色,然后将第一行涂成蓝色得到,若此时选择将第三列涂成绿色,则图中绿色方框中的格子都会变成绿色。

YZT 想用他自己编写的程序来进行视频中的游戏。在编程的过程中,YZT 在涂色逻辑的实现上却遇到了一些困难,于是他向你求助,希望你能帮他完成实现涂色逻辑部分的代码。
首先,YZT 会给你网格的行数和列数 $n, m$,然后给出 $q$ 次操作,每次操作用三个整数 $opt_i, x_i, c_i$ 表示:
- 如果 $opt_i=0$,那么这次操作会将第 $x_i$ **行**涂成颜色 $c_i$。
- 如果 $opt_i=1$,那么这次操作会将第 $x_i$ **列**涂成颜色 $c_i$。
在所有涂色操作结束以后,你需要输出网格中每个位置的颜色是什么。
输入
第一行包含三个整数 $n, m, q$,分别表示涂色板的行数、列数,以及 YZT 进行涂色操作的次数。
接下来 $q$ 行,每行包含三个整数 $opt_i, x_i, c_i$,表示一次操作。
接下来 $q$ 行,每行包含三个整数 $opt_i, x_i, c_i$,表示一次操作。
输出
对于每组数据,输出 $n$ 行,每行 $m$ 个由单个空格隔开的整数。
其中第 $i$ 行第 $j$ 个整数表示涂色完成后网格中第 $i$ 行第 $j$ 列的方格是什么颜色。
其中第 $i$ 行第 $j$ 个整数表示涂色完成后网格中第 $i$ 行第 $j$ 列的方格是什么颜色。
样例输入 复制
5 5 9
1 5 1
0 4 0
1 4 1
0 3 0
1 3 1
0 2 0
1 2 1
0 1 0
1 1 1样例输出 复制
1 0 0 0 0
1 1 0 0 0
1 1 1 0 0
1 1 1 1 0
1 1 1 1 1提示
### 样例输入 #2
```
3 3 3
0 1 2
0 3 1
1 1 3
```
### 样例输出 #2
```
3 2 2
3 0 0
3 1 1
```
**【数据范围】**
20%的数据满足:保证 $opt_i = 1$。
另20%的数据满足:保证 $opt_i = 0$。
100%数据,保证:
$1 \leq n,m \leq 10^3$,$0 \leq q \leq 10^6$,$0 \leq c_i \leq 10^9$。
若 $opt_i=0$,则 $1 \leq x_i \leq n$;若 $opt_i=1$,则 $1 \leq x_i \leq m$。
```
3 3 3
0 1 2
0 3 1
1 1 3
```
### 样例输出 #2
```
3 2 2
3 0 0
3 1 1
```
**【数据范围】**
20%的数据满足:保证 $opt_i = 1$。
另20%的数据满足:保证 $opt_i = 0$。
100%数据,保证:
$1 \leq n,m \leq 10^3$,$0 \leq q \leq 10^6$,$0 \leq c_i \leq 10^9$。
若 $opt_i=0$,则 $1 \leq x_i \leq n$;若 $opt_i=1$,则 $1 \leq x_i \leq m$。